|
|
「1999年 ICF3 暗号プロセッサ ゲートレベルの全設計図」のページを追加しました。ここから ハード編画像は、クリックすると拡大表示されます。 ハードウェアでは除算の性能を上げることが難しいことから、モンゴメリ乗算を用いて性能向上をするも、除算回路が全く不要になるわけではなく、いかに回路全体のゲート効率を短日程で改善するかが鍵だった。 全体図RSA演算器の全体図です。この図だけでマイクロコードが開発できます。いや、していました。 太線の四角の右下にCFXXXという名前があります。これはブロック名で1ブロック、約6000ゲート程度です。 (もう少し大きいゲート数のものもあります) 数字で0-63と書かれている場合は、そのブロックは64個のブロックに分割されていることを示しています。 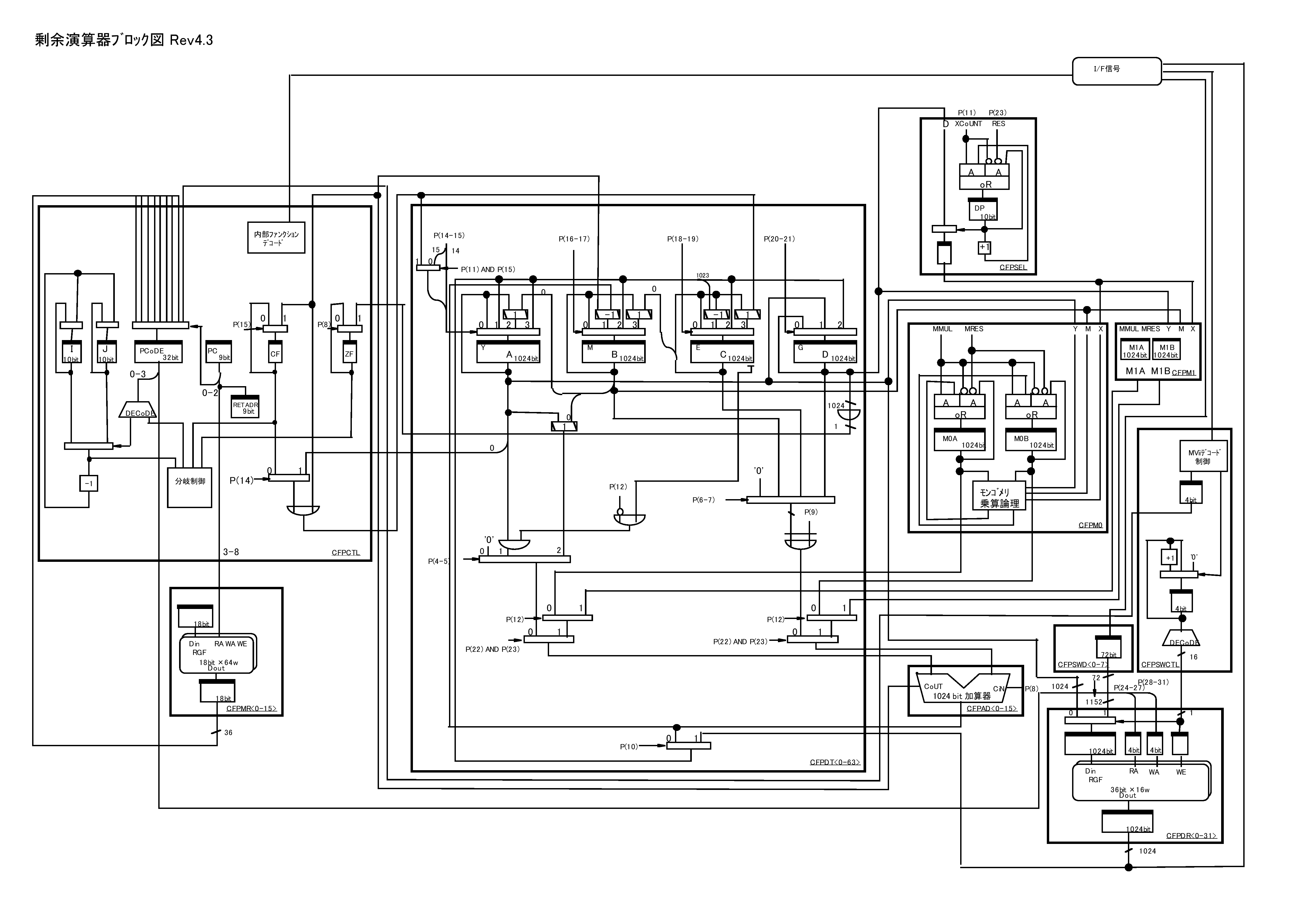
A、B、C、Dの1024ビットレジスタの入力側のセレクタ、出力側のセレクタを切り替えることで、 様々な動作が可能です。特筆すべき点はAレジスタのセレクト信号のセレクタであるP(11)という信号名です。 P(11)はマイクロコードの11bit目の信号ですがONにすると1024bit加算器のキャリーがAレジスタの入力セレクタの信号として入ってきます。 加算器のキャリーなので、多少ディレイが増加しますが、これにより1サイクルで比較して減算することが可能になっています。 ICF3はモンゴメリ乗算器を2個持っています。A×DとA×Aを同時に演算可能です。モンゴメリ乗算器を2個にしたのは性能上の問題からではなく制御論理を簡潔にしたかったからでした。マイクロコードが十分機能したので簡潔にすることに、こだわる必要はなかったということが後にわかった。しかし秘密鍵の値やモンゴメリ乗算のFinal Subtractionによって計算時間が変わることがないくRSAのタイミングアタックに対して強いという特徴を得ることにもなった。 ICF3のフロアプランLSI上にRSA演算器がどのように配置されているかが、わかると思います。 LSIの面積の半分近くをRSA演算器が占めています。 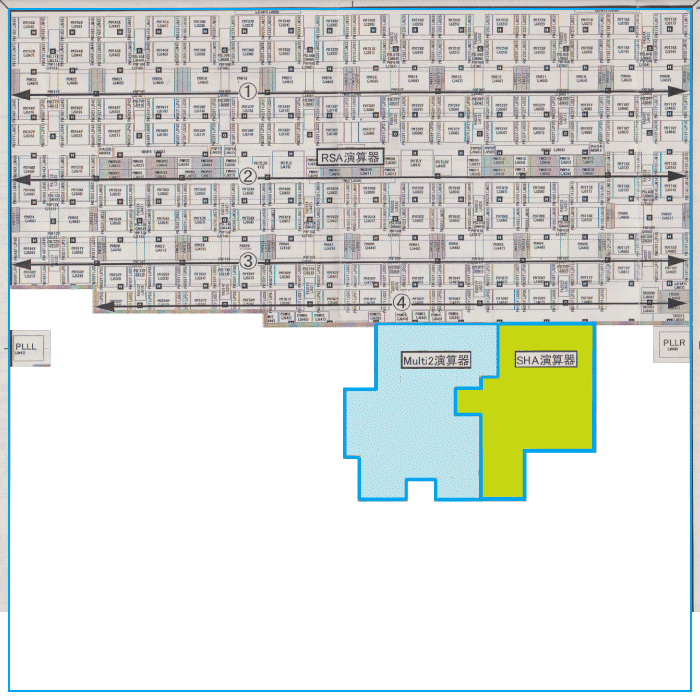
RSA演算器の配置図RSA演算器の各ブロックが、どのように配置されているかがわかる図です。 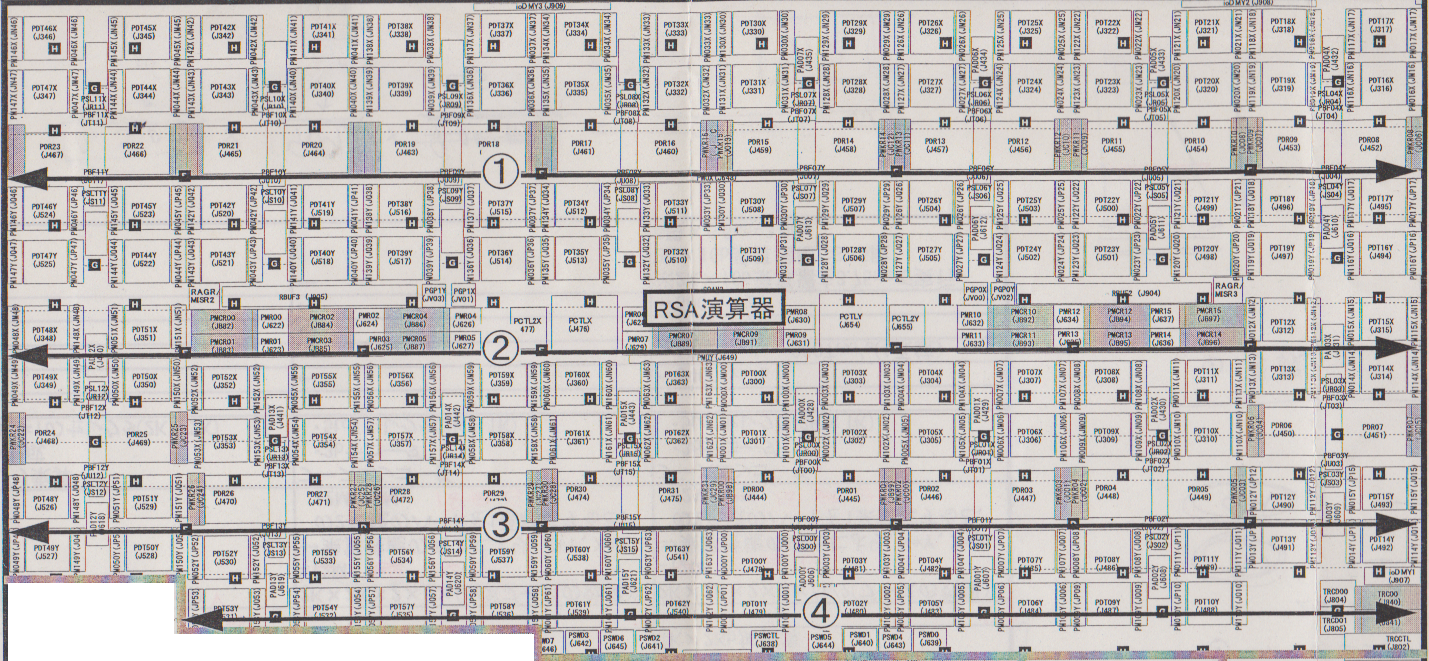
モンゴメリ乗算器の論理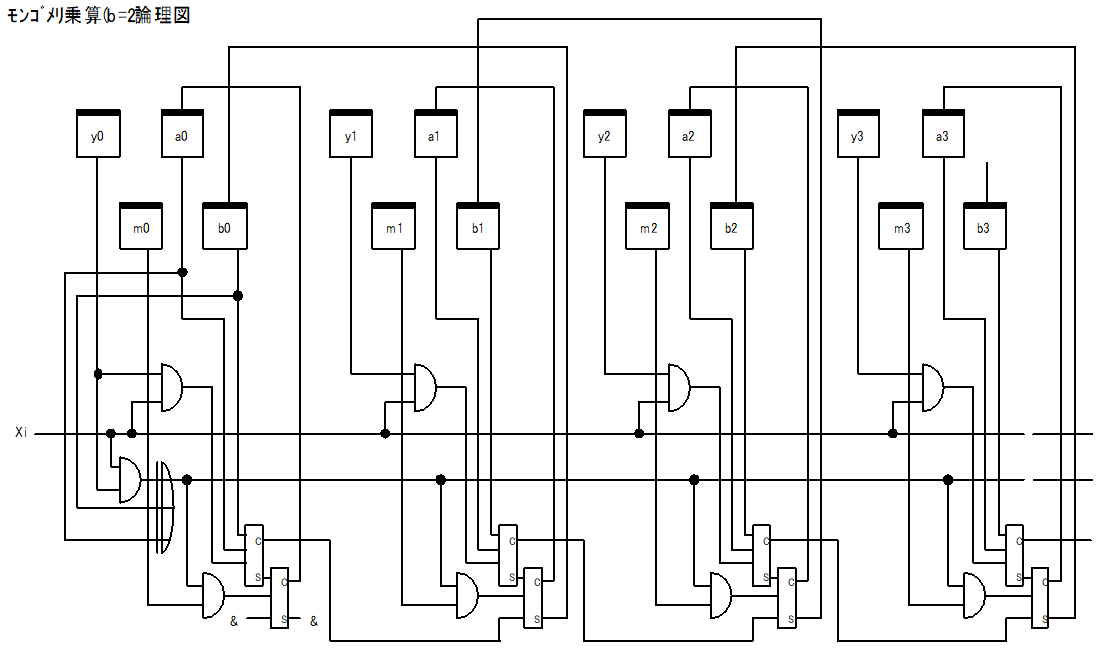
ゲート数ゼロの演算器1石2鳥の論理最適化によって、あり得ないゲート効率の演算器が作れることがあるかもしれない。
ゲート数ゼロのOR演算器は汎用的に使える技術なので覚えて損はしないかも。
1024bitのDレジスタの入力セレクタにゲート数ゼロのOR演算器がある。 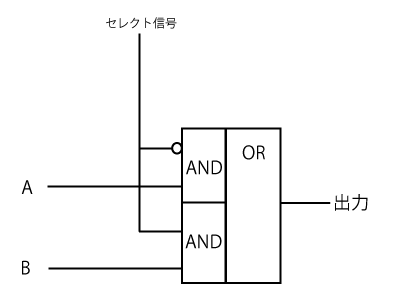
Dレジスタは3入力だが、セレクト信号は2本あるので4種類を表現できる。
1つ余るのでそこにAレジスタからの入力と加算器からの入力をORする機能を入れた。 これまでOR演算器を使用する暗号アルゴリズムはありませんでしたがRSA 4096bitで必要になりました。 簡素かつ組み合わせでいろいろな機能を実現できる設計思想の結果なのかもと。 いろいろな実装系に移植しやすい特徴LSIに実装するためには論理ゲートをブロックに分割してLSI平面上に配置しますが、 OpenICF3はブロックの種類が少ないため配置が容易です。 16bitのプロセッサを64個並べて1024bitのプロセッサとして動くような構造で、 暗号演算において隣接する近いデータだけで演算できるような構造になっています。 このため1024bit加算器などの限られたディレイに注意すれば良く配置が容易なのです。 LSI仕様FastMapとICF3の比較
今、改めて見てみて思うこと何もないところから、いきなりA、B、C、Dのレジスタの前後にあるセレクタが 自然に発生することはなく必要があって機能が追加されていったはずなのです。 今だとVHDLなどのハードウェア記述言語を使って簡単にシミュレーションできるので、 それほど難しいということはないかもしれないです。当時もVHDLのシミュレータは、あるには、 ありました。しかしVHDLを、それなりに勉強する時間が必要になってしまいます。 C言語で簡単に自作したシミュレータで機能を作りこめる能力が突貫工事を加速させることになったのだと思います。 当時の日立のハードウェア開発部のエンジニアは情弱でC言語ができる人がいなかった。 モンゴメリ乗算の原書を解読し、 不足分を補ってRSA暗号の演算方法を考えることができたのは、 やはりC++の多倍長演算のライブラリを使って、すぐに確認できたことも、大きかったのだとおもいます。 |

